See vastus pole midagi muud kui Sklivvi vastuse variatsioon. Ma soovin lihtsalt arutada mõningaid Sklivvi vastusest tulenevaid kvantitatiivseid ideid ja arutada, mida ma (lennunduse inseneri sõbralt) mõistan tavalise kontseptuaalse veana - et "lihtsalt pinnamõjude" ja "Bernoulli põhimõtte rakendamine" on vale. Need "pelgalt pinnaefektid ja Bernoulli põhimõte" tulenevad Sklivvi ideest, nagu ma loodan selgeks teha. Kõik lennukifüüsikas algab ja lõpeb "lennukid suruvad õhku allapoole, nii et õhk surub lennukid üles" . See vastus on kirjutatud arusaadavaks minusugusele, kes ei tea vedeliku dünaamikast midagi - välja arvatud:
-
Matemaatiliselt elegantsed ja igati nauditavad 2D-probleemid, mida lahendatakse keerulise muutujateooriaga (vt Stagnatsioonipunktide leidmine keerulisest potentsiaalist);
-
et ma tean, et igaühele, kes suudab tõestada selle olemasolu, on võimalik välja anda savimatemaatika auhind või anna vastunäide Navier-Stokesi võrrandite sujuvate, ülemaailmselt täpselt määratletud lahenduste olemasolu kohta;
-
et lennukitööstuse kolleegid ja sõbrad ütlevad mulle, et eksperimentaalne tõestus on selles valdkonnas endiselt kuninganna : enamik lennukilennuga kaasnevat reaalset vedeliku dünaamikat toetub suuresti eksperimentaalselt häälestatud fenomenoloogilistele mudelitele.
Vastan, tõstes need punktid järjest üles.
Katse on kuninganna
Konkreetsest eksperimentaalsest vaatenurgast , pole saladust, miks lennukid lendavad. Pigem on minu arvates parem küsimus: "kuidas nad kontrollivad nende vältimatuid tohutuid tõstejõude, et panna viimased stabiilselt püstises ja vertikaalses suunas üles tõusma?"
See eksperimentaalne vaade on järgmine: mõelge Beauforti skaalale ja teistele skaaladele, mida meteoroloogid kasutavad oma tuule ja muude hoiatuste praktilise tähenduse selgitamiseks: näiteks Fujita skaala tornaadode ja troopiliste tsüklonite kategooriasüsteemide jaoks, mis kirjeldavad praktiliselt erineva intensiivsusega tormide mõju.
Nüüd saan aru, et lennureeglid keelavad kommertslennukitel lennata aeglasemalt kui $ 300 \ mathrm {km \, h ^ {- 1}} $ enne lõplikku lähenemist rajale. Mõelge $ 300 \ mathrm {km \, h ^ {- 1}} $ õhukiirusele nende skaalade osas, millest ma just rääkisin: see on F4 tornaado, 5. kategooria tsüklon ja jääb 12-klassi Beauforti skaalast kaugele. Igasuguse kujuga ja täismassiga lennukite lennukid purustatakse ülespoole ja kantakse taevasse või purustatakse täielikult ja hävitatakse. $ 300 \ mathrm {km \, h ^ {- 1}} $ suhtelisel kiirusel ei ole lifti puudust, et hoida peaaegu kõike, mis on täielikult koormatud kommertslennuki suurus ja kaal: nendel lennukiirustel peaaegu kõik selle suuruse ja kaaluga ning kergemad kärbsed. Vähemalt teeb see seda üürikeselt: kui see pole disainitud nagu lennuk, muutub liikumise ajal tema suhtumine ja ka jäärasurve suund: siis on see tõenäoliselt ümber lükatud ja kriipsutatud katastroofiliselt maapinnale. Lihtsamalt öeldes: peaaegu kõik lendavad selle kiiruse juures, kuid ainult väga erilised asjad teevad seda stabiilselt.
lihtsad matemaatilised mudelid
Saame teha ümbrise hinnang rammusurvele sellisel juhul: vt allpool toodud joonist lihtsa aerofoili kohta, millel on märkimisväärne rünnakunurk ja mida hoitakse tuuletunnelis paigal. Panen Sklivvzi kirjeldusse mõned numbrid:
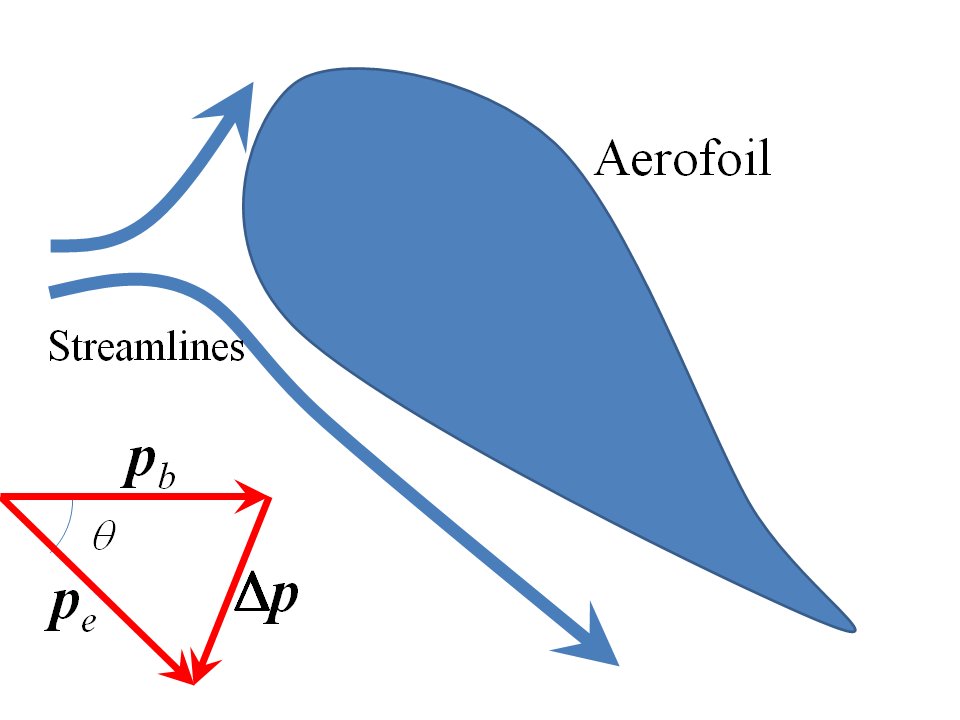
Oletame, et õhuvool suunatakse läbi $ \ theta $ radiaanide nurga alla, et modelleerida lennuki suhtumist (mitte kõrgust!) tema viimasel lähenemisel maandumisele või õhkutõusmisel lennates $ 300 \ mathrm {km \, h ^ {-1}} $ kiirus või umbes $ 80 \ mathrm {m \, s ^ {- 1}} $. Olen selle joonistanud järsu rünnakunurgaga. Merepinna atmosfäärirõhu lähedal oleva õhu tihedus on umbes 1,25 dollarit \ mathrm {kg \, m ^ {- 3}} $ (molaarne maht 0,0224 dollarit \ mathrm {m ^ {- 3}}) $. Kuvatakse impulsskeemi muutus, kust muutuvad vertikaalsed ja horisontaalsed impulsskomponendid (eeldades voolukiiruse püsimist ligikaudu konstantsena):
$$ \ Delta p_v = p_b \ sin \ theta; \ quad \ quad \ Delta p_h = p_b \, (1- \ cos \ theta) $$
Samal ajal pakub läbipaine tiib $ \ alpha \, A \ vedeliku jaoks efektiivse blokeerimisala , \ sin \ theta $, kus $ A $ on tiiva tegelik pind ja $ \ alpha $ skaalafaktor, et võtta arvesse asjaolu, et püsivas olekus hajutatakse mitte ainult tiiva kõrval asuvat vedelikku, nii et tiiva efektiivne ala olla suurem kui tegelik pind. Seetõttu on iga sekundi kõrvalekalduva õhu mass $ \ rho \, \ alfa \, A \, v \, \ sin \ theta $ ja tõstuk $ L $ ning lohista $ D $ (mis sunnib mootoreid õhkutõusmisel lubama) ) peab olema:
$$ L = \ rho \, \ alpha, A \, v ^ 2 \, (\ sin \ theta) ^ 2; quad \ quad D = \ rho \, \ alfa \, A \, v ^ 2 \, (1- \ cos \ teeta) \, \ sin \ teeta $$
Kui ühendame 30-kraadise rünnakunurga, eeldame, et $ \ alpha = 1 $ ja kasutame $ A = 1000 \ mathrm {m ^ 3} $ (umbes Airbusi A380 tiibapiirkonna näitaja), saame tõstejõud $ L $ for $ \ rho = 1.25 \ mathrm {kg \, m ^ {- 3}} $ ja $ v = 80 \ mathrm {m \, s ^ {- 1}} $ 200 tonni kaalust. See on pigem väiksem kui täielikult koormatud A380 Airbusi stardimass (mis on A380 Wikipedia lehe järgi 592 tonni), kuid see on hämmastavalt suur kaal sama ja õiges järjekorras suurusjärk. Nagu ma ütlesin, on siin kuninganna eksperiment. Me näeme, et tiiva efektiivne vertikaalne ristlõige on tegelikust tiibast suurem teguriga 2 kuni 3. See pole üllatav püsiseisundis, kõvasti alla helivoolu kiiruse: vedelik koguneb ja häire on palju suurem kui lihtsalt tiiva naabruses. Niisiis, pistikupesa $ \ alpha = 3 $ ühendamisel (arvestades eksperimentaalset fakti, et A380 võib tõusta 592 tonnise täismassiga), saame lohistamise D $ $ 54 tonni kaalust (538 kN) - umbes poole Airbusi täistõmme 1,2 MN, seega sobib see hästi kokku Airbusi tegelike spetsifikatsioonidega, kuna peab olema mugav varu, et lennuk vajadusel raskustest välja tõsta.
Nendes F4 / C5 klassi tuultes (ja kuni kolm korda kiiremini kui tavaline lend), näeme seetõttu, et liftist pole lihtsalt puudust. Lennundustehnika probleem seisneb pigem selles, et hoida seda ohtrat lifti stabiilselt ülespoole ja võimaldada lennukil püsida kindlalt ning hoida kõik lifti ebaühtlusest tulenevad pöördemomendid lennukist ümber.
Lennuki kiiruse suurenedes on ülalpool arvutatud tõukurõhk proportsionaalne lennukiiruse ruuduga (vt minu vastust lohisemisjõule suurtel kiirustel), nii et täiskiirusel mõjuks rohkem kui õhutiheduse langus ja madalam rünnakunurk - me ei saa seda allapoole jäävat rõhku teha, ületamata palju suuremat horisontaalset tagumist komponenti - lohistamist -, nii et hea kütusesäästlikkuse huvides on oluline lennata madala rünnakunurgaga / p>
Matemaatilise mudeli täpsustamine
Oluline on arvestada, et ülaltoodud kirjeldus sissetuleva õhu ja tiiva tekitatud allavoolu vahelise impulsside erinevuse osas on täpselt sama füüsika kui "populaarsemad" kirjeldused, mis on antud Bernoulli võrrandi ja tiiva ümber oleva rõhu integreerimise osas. Seda on lihtne mõista: Navier-Stokesi võrrand ( Navier-Stoksi võrrandi tuletamiseks vaadake Wikipedia lehte) on väga lihtne rakendus, mis pole midagi muud Newtoni teine ja kolmas seadus lõpmatusse vedeliku hulka, hoolimata teadmiste puudumisest selle põhiliste matemaatiliste omaduste kohta (nagu ütleb Clay Mathematics Millenium Prize'i nõutav staatus: ma armastan Navier-Stokesi võrrandit - nii lihtne, hõlpsasti mõistetav idee nii kiilas lihtsalt Newtoni seaduste kehastus, visates siiski sügavaid saladusi, mis näitavad meile teadlastele, kui vähe me veel maailmast teame). Püsiseisundi Navier Stokesi võrrand täiusliku, kokkusurumatu vedeliku jaoks on (siin on $ \ vec {v} $ püsiseisundi kiirusväli ja $ p $ skalaarrõhuväli):
$$ (\ vec {v} \ cdot \ nabla) \ vec {v} = \ nabla \ left (\ frac {| \ vec {v} | ^ 2} {2} \ right) + \ nabla \ wedge (\ nabla \ wedge \ vec {v}) = - \ nabla p $$
mis annab $ \ nabla \ left (p + \ frac {| \ vec {v} | ^ 2} {2} \ right) = 0 $ või $ p + \ frac {| \ vec {v} | ^ 2} {2} = \ text {const} $ irrotatsioonivoo jaoks ($ \ nabla \ wedge \ vec {v} = \ vec {0} $) integreerituna piki $ \ vec {v} $ integraalkõverat, st sujuvamaks. Või võime sel lihtsal juhul vaielda esimesel põhimõttel: lõpmatuima mahu jõud on $ - \ nabla p $ ja osakese kiirendus voolujoonel on Serret-Freneti valemite abil (siin on $ s $ kaare pikkus sujuvalt läbi osakese ja $ \ kappa $ tee kõverus):
$$ \ mathrm {d} _t (v \ hat {\ mathbf {t} }) = \ mathrm {d} _s v \ times \ mathrm {d} _t s \, \ hat {\ mathbf {t}} + v \, \ mathrm {d} _s (\ hat {\ mathbf {t}} ) \, \ mathrm {d} _t s = v \, \ mathrm {d} _s v, \ hat {\ mathbf {t}} - \ kappa \, v ^ 2 \, \ hat {\ mathbf {n}} = \ mathrm {d} _s \ left (\ frac {v ^ 2} {2} \ right) \, müts {\ mathbf {t}} - \ kappa \, v ^ 2 \, \ hat {\ mathbf { n}} $$
kust $ \ vec {F} = m \ vec {a} \ Rightarrow - \ nabla p \, \ mathrm {d} x \, \ mathrm {d} rakendamisel y \, \ mathrm {d} z = \ rho \, \ vec {a} \, \ mathrm {d} x \, \ mathrm {d} y \, \ mathrm {d} z $, saame:
$$ - \ nabla p = \ rho \ left (\ mathrm {d} _s \ left (\ frac {v ^ 2} {2} \ right) \, \ hat {\ mathbf {t}} - \ kappa \, v ^ 2 \, \ hat {\ mathbf {n}} \ right) $$
mis jällegi annab $ p + \ frac {| \ vec {v} | ^ 2} {2} = const $, kui see on integreeritud mööda voolujoonelist (siin näeme külgsuunas (normaalne kuni sujuvamaks) tsentraalset jõudu $ -v ^ 2 \, \ hat {\ mathbf {n}} / R $, mille annab tavaline valem $ v ^ 2 / R $). Seega võime (ja allpool) rakendada tõusu arvutamiseks näiteks Blasiusi teoreemi ja olla kindel, et see on ainult kvantifitseerimine Sklivvi ideest, et "lennukid suruvad õhku allapoole, nii et õhk surub lennukid üles ". Rõhu erinevus tiiva ülemise ja alumise pinna vahel on olemas kuna tiib surub õhku alla, mitte eraldi nähtus. Sageli kuuleb, et tiibadele rakendatud Bernoulli põhimõte on vale: see pole tõsi. Bernoulli põhimõtet järgides on tõsi (mida käsitletakse allpool) eksituse näol (mida käsitletakse allpool - teooriaga) lifti tavapärasel demonstreerimisel, kuid idee on põhimõtteliselt kindel, kuna see peab tulenema selle tuletamisest Navier-Stokesi võrrand ja ülaltoodud Newtoni seadused.
Joukowsky aerofoili arvutamine ja vead Bernoulli põhimõtte tahtmatul kasutamisel tiibadele
Vaatame lifti kahemõõtmelist arvutamist Bernoulli põhimõtte järgi või samaväärselt Blasiuse teoreemi rakendamisega. Levinud väärarusaam on see, et õhuvoolud jagunevad tiiva esiservas ja kaks naaberosakest jõuavad üheaegselt tiiva mahajäänud servani, nii et ülemised osakesed peavad kõverdunud pinda maksma suurema kiirusega ja seetõttu surve ülemisele tiiva pinnale on vähem. Tegelikult kiirendatakse ülemise tee osakesi palju rohkem, kui see selgitus eeldab, ja jõuavad tiiva mahajäänud servani tublisti enne nende alumist rada läbivat naabrit. Vaadake seda imelist videot Cambridge'i ülikoolist, eriti umbes 50 sekundi pärast. See fakt näitab, et tiraaž $ \ lub_ \ Gamma \ vec {v} \ cdot \ mathrm {d} \ vec { r} $ ümber tiiva pinna $ \ Gamma $ ei ole null, see on fakt, mida eeldame intuitiivselt lihtsalt teoorialt (nagu allpool näidatud) ja mis on katses piisavalt kinnitatud: vaadake videot või minge maandumisraja lõppu niiskel päeval suur lennujaam, et saaksite lasta suurtel kommertslennukitel umbes 50m kõrgusel enda kohal lennata (võtke kõrvaklapid). Niiskel päeval näete keeriseid, mis murravad tiibade välisservad, näete neid mitu sekundit niiskes õhus keerlemas lennuki ärkvel ja kui võtate kuulmiskaitsevahendid pärast lennuki möödumist maha, kuulete õhus kärisevad keerised, mis kõlavad veidi nagu rannas pesevad lained. See on palju lõbusam, kui see kõlab, kui teie lapsed mäkerdavad teid sellist asja tegema ning vaatamisväärsuste ja helide põhjal õppisin ma seda tehes veel palju, mida arvasin. Kuigi järgmisel arvutusel on teoreetiline usaldusväärsus ja "esimesed põhimõtted", on oluline mõista, et ka see on eksperimentaalne mudel : tiraaž sunnitakse meie kirjeldusse, motiveerituna esimese olemasolu kinnitamine eksperimendiga. Kutta-Joukowski tingimus (vt Kutta tingimuse Vikipeedia lehte) kui ka Kutta-Joukowski teoreemi Wikipedia leht on midagi muud kui ad hoc eksperimentaalselt motiveeritud lahendus : see on lihtsalt see. Kui voolu modelleerime aerofoiliga Joukowski (kirjeldatud allpool), on tiival terav, mahajäänud serv. See tekitab ebafüüsikaliste, lõpmatute kiirustega singulaarsuse. Postuleerides ja voolus õige ringluse valides võime aga panna stagnatsioonipunkti mahajäänud serva, tühistades seeläbi singulaarsuse, seadustades meie lahenduse ja sundides ka eksperimentaalselt täheldatud tingimust, et tiiva juures on alati ainult üks stagnatsioonipunkt esiserv, mitte kunagi mujal.
Veel üks viis selle eksperimentaalselt motiveeritud seisundi vaatamiseks on selles vastuses füüsika SE küsimusele kas potentsiaalse voo tiib tõuseb? on hästi selgitatud. Irrotatsiooniline, nähtamatu, kokkusurumatu vool ei saa üksi tiiba üles tõsta. Selle teoreetilise puuduse kompenseerimiseks lisame ringluse, et kompenseerida: viskoossus on "looduse viis Kutta-Joukowsski tingimuse jõustamiseks".
Nii et alustame keerulise muutuja meetodiga (vt Wikipedia "Potentsiaalse voo" leht jaotises "Kahemõõtmelise voo analüüs" potentsiaalse voo uurimiseks, st irrotatsiooniline ($ \ nabla \ wedge = \ vec {0} $) kiirusväli $ \ vec {v} $ potentsiaaliga $ \ psi $, nii et $ \ vec {v} = - \ nabla \ psi $, mis on samuti kokkusurumatu (järjepidevuse võrrand $ \ nabla \ cdot \ vec {v} = \ nabla ^ 2 \ psi = 0 $ ). Vaadake ka Physics SE küsimusi Stagnatsioonipunktide leidmine komplekspotentsiaalist).
Siin on peamine meetod kasutada Joukowski teisendit:
$ $ \ omega (z, \, s_z, \, s_ \ omega) = \ frac {s_ \ omega} {2} \ vasakule (\ frac {z} {s_z} + \ frac {s_z} {z} \ paremale) $$
pöörleva, nihutatava silindri ( vaadake NASA lehte „Pöörleva silindri tõstmine”) vastava potentsiaalse voolu kaardistamine selle silindri kujutise ümber voolu Joukowsky teisenduse all. tõeliselt imelik Flettneri lennuk kasutas edukaks lendamiseks tegelikult tiibade asemel pöörlevaid silindreid. Joukowsky teisendus kaardistab ringi $ | z | = s_z $ reaalsele teljele punktide $ \ omega = \ pm s_ \ vahel omega $ lennukis $ \ omega $; see reaaltelje osa $ \ omega = \ pm s_ \ omega $ vahel on siis haru, mis on lõigatud pöörd-Joukowski teisenduse jaoks. Joukowsky teisendus on kaardistamine kaks ühele ja pöördtransformaadi Joukowski transformatsiooni harud kaardistavad kogu $ \ omega $ -Riemanni sfääri (kui defineerida stereograafiline projektsioon nii, et $ | z | = s_ \ omega $ on $ \ omega $ -Riemanni sfääri ekvaator) eraldi sisemusse ja väljaspool ringi $ | z | = s_z $ lennukis $ z $ (mida väljast ja seest võib mõelda põhja- ja lõunapoolkeral sfääri $ z $ -Riemann, kui stereograafiline projektsioon on valitud nii, et ring $ | z | = s_z $ on sfääri $ z $ -Riemann ekvaator). Pind $ \ omega $ -Riemann tehakse nii, et lõigatakse kaks Riemanni sfääri koopiat mööda lõigatud haru ja õmmeldakse servad kokku, et saada sfäärile $ \ omega $ -Riemann sile kahekordne kate. Selle probleemi jaoks määratlen haru, mis on lõigatud veidi erinevalt tegeliku telje sektsioonist $ \ pm s_ \ omega $ vahel, määratlen selle kui tee:
$$ \ operaatori nimi {Im} (\ omega) = h \ cos \ left (\ frac {\ pi} {2} \ operaatori nimi {Re} (\ omega) \ right) $$
kahe harupunkti vahel reguleeritava kõrguse parameetriga $ h $, selguvatel põhjustel.
Keeratava silindri raadius raadius $ r $ valitakse nii, et silindri pind läbiks punkti $ z = + s_z $, mis on ühe $ \ omega $ tasapinna harupunkti pilt. Sellega saavutatakse terav serv, millest saab meie aeropurje mahajäänud serv.
Keeratava silindri kompleksne potentsiaal on järgmine:
$$ \ Omega (z) = v \, e ^ {- i \ alpha} \, \ left (z- \ delta \ right) + \ frac {r ^ 2 \, v \, e ^ {+ i \ alpha}} {z- \ delta} + i \, a \, \ log \ left (z - \ delta \ right) $$
kus $ \ alpha $ on rünnaku nurk, $ \ delta = \ delta_r + i \, \ delta_i $ on nihe ja $ r $ on silindri raadius, mis on immutatud ühtlasesse voolu, mis koondub $ v $ meetrit sekundis piki positiivset tegelikku telge, kui $ z \ kuni \ infty $. Logaritmi ja dipooli mõisted asetavad silindri keskele hargnemispunkti ja pooluse, nii et voog sobib ideaalselt silindrist väljapoole ja peale. $ a $ on tiraaž. Kui laseme $ \ phi $ tähistada silindri serva märgistavat nurgakoordinaati, on silindris kaks nurkkoordinaatidega stagnatsioonipunkti $ \ phi_ \ pm $, kus $ \ mathrm {d} _z \ Omega (z ) = 0 $, ie millal:
$$ e ^ {i \, (\ phi_ \ pm - \ alpha)} = -i \ frac {a} {2 \, v \, r} \ pm \ sqrt {1- \ left (\ frac {a} {2 \, v \, r} \ right) ^ 2} = \ exp \ left (- \ arcsin \ frac {a } {2 \, v \, r} \ right) $$
Nüüd kaardistame selle voo $ \ omega $ tasapinnale ja rakendame Blasiuse teoreemi nihverõnga pilt, et selle pildi tõstmiseks välja töötada. Pilti saab joonistada käsuga Mathematica:
$$ \ small {\ mathrm {P [\ delta_r \ _, \ delta_i \ _]: = \\ ParametricPlot [\ {Re [\ omega [ \ delta_r + i \ delta_i + \ sqrt {(1 - \ delta_r) ^ 2 + \ delta_i ^ 2} Exp [i \ theta]], Im [\ omega [\ delta_r + i \ delta_i + \ sqrt {(1 - \ delta_r) ^ 2 + \ delta_i ^ 2} Exp [i \ theta]] \}, \ {\ theta, 0, 2 \ pi \}]}} $ $
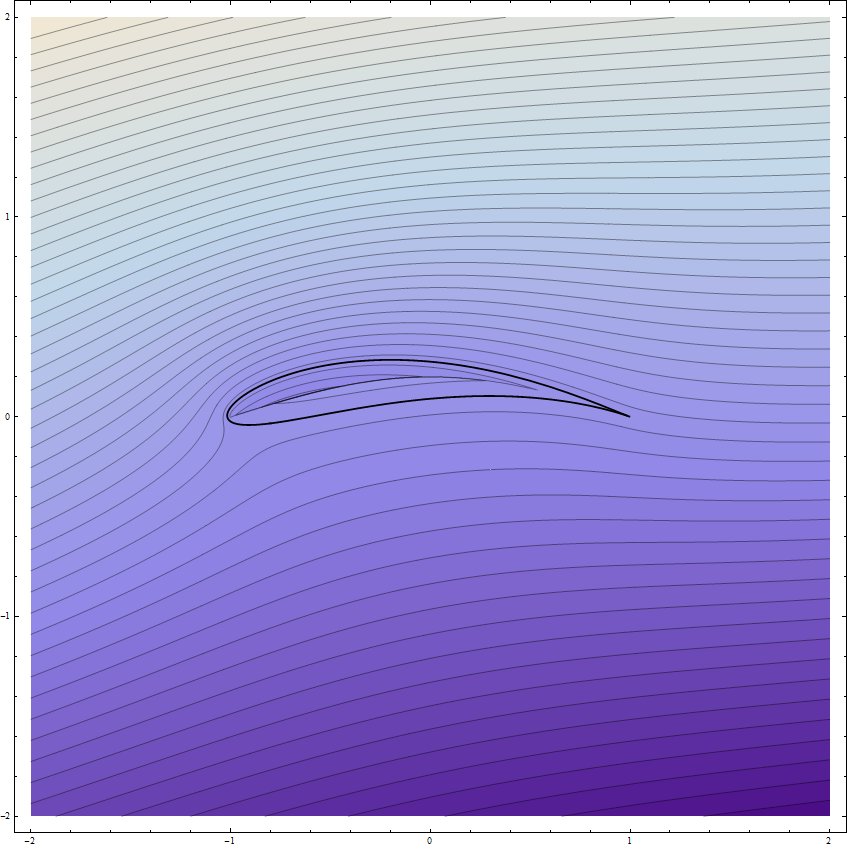
ja tulemus on joonistatud allpool $ \ omega $ -tasandil $ s_z = s_ \ omega = 1 $, $ \ delta_r = -0.1 $, $ \ delta_i = 0.3 $ ( ie pöörlev ring nihkub nii, et keskel on $ -0.1 + i \, 0.2 $ ja raadiusega $ r = \ sqrt {(1 - \ delta_r) ^ 2 + \ delta_i ^ 2} $, nii et selle pilt läbib hargnemispunkti $ \ omega = + s_ \ omega = 1 $ lennukis $ \ omega $:

Nüüd jõuame üliolulise Kutta-Joukowski postulaadi juurde, eksperimentaalse "fudži" juurde. Ülaloleva aerofoili terav serv kaardistab tavaliselt $ z $ -tasandi voolu nii, et selles teravas punktis oli ebafüüsiline lõpmatu kiirus. Praktikas on tuuletunneli katsetel näha, et voolujooned jäävad puutuma ülemist pinda ja tiiva esiservas on üks stagnatsioonipunkt (siin intuitiivselt õhk "kokku kukub") ja pole ühtegi teist tugevat > stagnatsioonipunktid kas tiiva alaosas ülaosas. Mõnikord on tiiva mahajäänud serva ümber väike turbulentsi piirkond (nagu Cambridge'i ülikooli videos) (st kokkusurumatu potentsiaalse voolu mudel ebaõnnestub siin) või voolab koor sujuvalt maha mahajäänud servast. Eksperimentidega sarnanevate efektide saavutamise ja meie lahenduse renormaliseerimise viis on lisada vooluhulgale õige kogus tsirkulatsiooni $ a $, nii et ketrussilindri üks stagnatsioonipunkt oleks kaardistatud terava servaga (hargnemispunkt $ \ omega = + s_ \ omega $) lennukis $ \ omega $: stagnatsioon tühistab seeläbi muidu ebafüüsilised lõpmatud kiirused ja "seadustab" meie lahenduse. Kui silindri raadius on valitud $ r = \ sqrt {(1 - \ delta_r) ^ 2 + \ delta_i ^ 2} $, saab ülaltoodud võrrandist stagnatsioonipunktide positsioonide jaoks hõlpsasti näidata, et vajalik ringlus on:
$$ a = 2 v \, \ delta_i \ cos \ alpha + 2 \, v \, (1- \ delta_r) \ sin \ alpha $$
See on siis eksperimentaalselt motiveeritud Kutta-Joukowski seisund. Selle ajendiks on teadmine, et vereringet vaadeldakse noorsetes tiibades, tiiva esiservas on eksperimentaalselt ainult üks stagnatsioonipunkt ja asjaolu, et õige koguse vereringe abil saab neid katseliselt nähtud tulemusi korrata
Kui see on tehtud, on $ \ omega $-lennukis ümberkujundatud Joukowski aerofoili ümber tehtud Blasiuse teoreemi tõusu arvutus:
$$ \ begin {array} {lcl} D_ \ ell - i \, L_ \ ell & = & \ frac {i \, \ rho} {2} \ lub _ {\ Gamma_ \ omega} (\ mathrm { d} _ \ omega \ Omega) ^ 2 \, mathrm {d} \ omega \\ & = & \ frac {i \, \ rho} {2} \ lub _ {\ Gamma_z} (\ mathrm {d} _z \ Omega) ^ 2 \ frac {1} {\ mathrm {d} _z \ omega} \, \ mathrm {d} z \\ & = & - \ pi \, \ rho \ Sigma [\, \ mathrm {jäägid \, \,} \, (\ mathrm {d} _z \ Omega) ^ 2 \ frac {1} {\ mathrm {d} _z \ omega} \, \ mathrm {at \, poolused \, \,} \ Gamma ] \\ & = & -4 \, \ pi \, i \, \ rho \, a \, v \, e ^ {- i \, \ alpha} \ end {array} $$
kus $ \ Gamma_ \ omega $ on Joukowski aerofoil ja $ \ Gamma_z $ transformeeritud aerofoil ( ie pöörlev silinder). Nii et ilma ringluseta lifti pole. Tasub uuesti öelda:
Irrotatsiooniline, nähtamatu, kokkusurumatu vool ei saa üksi tiiba tõsta. Selle teoreetilise puuduse kompenseerimiseks lisame ringluse, et kompenseerida: viskoossus on "looduse viis Kutta-Joukowsski tingimuse jõustamiseks".
Nüüd asendame Kutta-Joukowski tingimuse, et saada:
$$ D_ \ ell + i \, L_ \ ell = 8 \, \ pi \, i \, \ rho \, v ^ 2 \, \ left (\ delta_i \, \ cos \ alfa + (1- \ delta_r) \, \ sin \ alpha \ right) \ frac {s_z ^ 2} {s_ \ omega} e ^ {+ i \ alpha} $$
Peame nüüd mõõtkava muutma kiirused nii, et suhtelised lennukiirused oleksid $ \ omega $ - ja $ z $-lennukites võrdsed.
Ülaltoodud on jõud tiiva pikkuseühiku kohta (lehe suhtes normaalses suunas) ja selle suund on $ \ omega $ -tasandi suund. Meil on:
$$ \ lim \ limits _ {\ omega \ to infty} \ left (\ mathrm {d} _ \ omega \ Omega (\ omega (z)) \ right) = \ lim \ limits_ {z \ to \ infty} \ left (\ mathrm {d} _z \ Omega (\ omega (z)) \ right) \ lim \ limits _ {\ omega \ to \ infty} \ left (\ mathrm {d} _ \ omega z \ right) = 2 \, e ^ {- i \ alpha} v \ frac {s_z} {s_ \ omega} $$
nii et meil on vaja $ s_ \ omega = 2 $ ja $ s_z = 1 $, siis on $ \ delta $ dimensioonitu parameeter, mis määratleb $ z $ -tasandi silindri nihke murdosa selle raadiusest. Nüüd on tiiva $ \ omega $ -planeeringu kuju laius 4 ühikut. Veelgi enam, ülaltoodud arvutus annab jõu pikkuse ühiku kohta (normaalne 2D voolu suhtes). Niisiis jagame tulemuse $ s_ \ omega = 2 $ ja $ s_z = 1 $ väärtusega 4 ning suurendame siis tiiva kogupindala järgi, et saada tiibale kogu jõud. Lisaks peame voolu allpool oleval joonisel pöörama nii, et sissetulev voog oleks horisontaalne (st lennuki suhtelise õhukiiruse suunas), kui ülemise tiiva $ \ omega $ summaarne jõud muutub:
$$ D + i \, L = \ pi \, i \, \ rho \, v ^ 2 \, A \, \ left (\ delta_i \, \ cos \ alpha + (1- \ delta_r) \, \ sin \ alpha \ right) $$
Oleme tunnistajaks d'Alemberti paradoksile: täiuslik voog ei saa lohistamist modelleerida. Nüüd paneme mõned numbrid sisse. Kui paneme $ \ delta = 0 $, siis on tiib lihtsalt sirge haru, mis on lõigatud vahemikku $ \ omega = \ pm 1 $, nii et meil on versioon arvutusest, millega alustasin, kuid nüüd täpsustasin et võtta arvesse kogu voolu mustrit. Kui $ \ alpha = 0.3 $ (veidi alla 20 kraadi), $ \ rho = 1.25 \ mathrm {kg \, m ^ {- 3}} $, $ v = 80 \ mathrm {m \, s ^ {- 1}} $ ja $ A = 850 \ mathrm {m ^ 2} $, saame $ L = 643 \ mathrm {tonne} $, mis on üsna lähedal Airbusi täielikult koormatud stardikaalule. Kui valisime parameetrid $ \ delta_i = 0.2 $, $ \ delta_r = -0.1 $, et anda tiiva kuju, mis ei tundu jetlineri tiiva jaoks liiga väljamõeldud, kui mahajäänud servaklapid olid õhkutõusmiseks ja maandumiseks täielikult välja keeratud (vt joonist allpool) saame $ 1200 \ mathrm {km \, h ^ {- 1}} $ kiiruse eest umbes 1200 tonni tõste. Ilmselgelt on see optimistlik ja üleliigne seos tuleneb eeldusest, et kogu tiibade siruulatus on võrdne, samas kui näpunäiteid ei saa 2D-voog selgelt hästi modelleerida. Kõik tiivad ei tööta modelleerituna, seega on selles valemis $ A $ mõnevõrra väiksem kui plaanikujuline ala. Voolumudel näitab (vt allpool) aga seda, et sissetulevale õhule esitatav efektiivne vertikaalne ristlõige on palju suurem kui alguses väga lihtsas mudelis eeldatav kallutatud ala $ A \, \ sin \ theta $ minu vastusest. Püsiseisundis on märkimisväärne õhu ristlõige nii vertikaalse ristlõike kohal kui ka allapoole painutatud allapoole ja aitab kaasa Sklivvi vastuses kirjeldatud efektile "lennukid suruvad õhku alla, nii et õhk surub lennukid üles".
Nüüd, kui plaanida $ \ omega $ -tasandisse kogu teisendatud voog joonistada, peame kasutama Joukowski pöördteisendit. Et seda edukalt teha, tuleb kasutada pöördtransformatsiooni õigeid harusid õigetes koordinaatplaastrites. Mathematica jaoks, mis asetab ruutjuure funktsiooni jaoks lõigatud haru reaalteljele negatiivne (nimeruum std :: sqrt rakenduses Microsoft Visual C ++ asetab selle reaalsele teljele positiivne ), määratleme järgmised diagrammifunktsioonid, mis on pöördtransformatsiooni konkreetsed harud:
$$ \ zeta_1 (\ omega) = \ frac {s_z} {s_ \ omega} \ left (\ omega- i \ sqrt {\ omega-s_ \ omega} \, \ sqrt {- \ vasakule (\ omega + s_ \ omega \ paremale}} \ paremale) $$$$ \ zeta_2 (\ omega) = \ frac {s_z} { s_ \ omega} \ left (\ omega + i \ sqrt {\ omega-s_ \ omega} \, \ sqrt {- \ left (\ omega + s_ \ omega \ right)} \ right) $$$$ \ zeta_3 (\ omega) = \ frac {s_z} {s_ \ omega} \ left (\ omega- \ sqrt {\ omega ^ 2-s_ \ omega ^ 2} \ right) $$$$ \ zeta_4 (\ omega) = \ frac { s_z} {s_ \ omega} \ left (\ omega + \ sqrt {\ omega ^ 2-s_ \ omega ^ 2} \ right) $$
ja seejärel joonistavad järgmised Mathematica käsud kogu voo:
$$ \ small {\ mathrm {\ Omega [z \ _, \, \ delta \ _, \, v \ _, \, r \ _, \, a \ _, \, \ alfa \ _, \, s \ _]: = v \, e ^ {- i \, \ alfa} \ vasakule (\ frac {z} {s} - \ delta \ right) + \ frac {r ^ 2 \ , v \, e ^ {i \, \ alpha}} {\ frac {z} {s} - \ delta} + i \, a \, Logi \ vasakule [\ frac {z} {s} - \ delta \ right]}} $$$$ \ small {\ mathrm {G [z \ _, \, \ delta_r \ _, \, \ delta_i \ _, \, \ alfa \ _]: = \ Omega vasakule [z, \, \ delta_r + i \, \ delta_i, \, 1, \, sqrt {(1- \ delta_r) ^ 2 + \ delta_i ^ 2}, 2 \, \ delta_i Cos [\ alpha] + 2 \, (1- \ delta_r) \, Sin [\ alfa], \, \ alfa, \, 1 \ right]}} $$
$$ \ small {\ mathrm {S [\ delta_r \ _, \ delta_i \ _, \ alpha \ _, h \ _, c \ _]: = \\ Kuva [ContourPlot [Im [Kui [(Abs [x] < 1) \ kiil (y > 0) \ kiil (y < h \, Cos [\ pi x / 2]), G [\ zeta_1 [x + iy], \ delta_r, \ delta_i, \ alpha]], Kui [x < 0, G [\ zeta_3 [x + iy], \ delta_r, \ delta_i, \ alpha]], G [\ zeta_4 [x + iy], \ delta_r, \ delta_i, \ alfa ]]]]], \ {x, -2, 2 \}, \ {y, -2, 2 \}, kontuurid \ to c, MaxRecursion \ to 2, PlotPoints \ to 300, AspectRatio \ to 1],
P [\ delta_r, \ delta_i, \ {must, paks \}]]}} $$
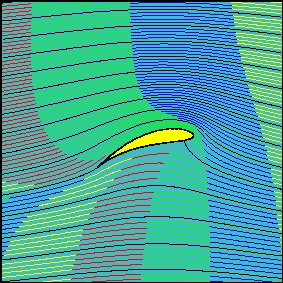
kus $ \ mathrm {P} [] $ on ülaltoodud parameetriline jooniskäsk, mida kasutatakse tiiburiku joonistamiseks. Ülaltoodud harufunktsioonide kasutamine töötab $ \ delta_r < 0 $ puhul: õigete tulemuste saamiseks on vaja muid harusid, kui $ \ delta_r > 0 $. Parameeter $ h $ painutab lõigatud haru nii, et see kummardub ülespoole ja jääb aerofoili sisse, võimaldades seeläbi pöörd-Joukowsky transformatsiooni harudel kaardistatud silindri voogu korralikult joonistada. Allpool on joonistatud käsu $ \ mathrm {S [-0,1, 0,2, 0,2, 0,2, 100]} $ tulemus, ie voog tiiva ümber 0,2 radiaani rünnakunurga korral, ringi nihke parameetrid $ -0,1 + 0,2 \, i $, vibu oksas lõigatud nii, et $ h = 0,2 $. Tunnista haru, mis on allpool aerofoili sisse lõigatud, ja ka seda, kui kaugel tiiva pinnast selle mõju ulatub. Tiiva ala efektiivne vertikaalne komponent, mis esitatakse vooluhulgale, on selgelt palju suurem kui tiiva tegelik vertikaalne komponent, seega näib A380 Airbusi lifti skaleerimise tegur 2 kuni 3 lihtsa vedeliku painde arvutamise abil väga usutav ja üllatav.
Lõpuks, et tulla kogu ring, on siin animatsioon, mida leiate veebilehtedelt "Invisitsiidse vedeliku irrotatsioonilised tasapinnavood" Genova ülikooli keskkonnatehnika osakond; vaadake http://www.diam.unige.it/~irro/. Animatsioon näitab Joukowski aerofoili voolu vedelike osakeste kulgu, illustreerib väidet, et tiiva kohal olev voog läbib tiiba palju kiiremini kui all olev vool ja viimasena näitab väga hästi põhiteesi, et "lennukid suruvad õhku allapoole".